Double this for a denominator of 4a Put them together, and this gives you the formula for kExplore the parent graph y=x^3 Experiment with the values of a, h, and k What happens to the graph as these values change?X kis the solution 2 Compute a search direction Compute the vector p kthat de nes the direction in nspace along which we will search 3 Compute the step length Find a positive scalar, ksuch that f(x k kp k)

3 Ways To Find The Inverse Of A Quadratic Function Wikihow
A(x-h)^2+k how to find a
A(x-h)^2+k how to find a-I will answer this way, since I suspect you're preparing for finals The x and y are the variables They aren't replaced with specific numbers in the equation unless you are finding (x, y) coordinates for points on the parabola The h is a horizonTo do this, we are going to use the method of completing the square Standard form of a quadratic equation is y=ax 2 bxc, where 'a' is not 0 Vertex form of a quadratic equation is y=a (xh) 2 k, where (h,k) is the vertex of the quadratic function 'a',



Graphing Quadratic Functions
Answer to Write the quadratic function in the form f(x)= a(x h)^2 k Then, give the vertex of its graph f(x)= 2x^2 4x 4 By signing up, for Teachers for Schools for Working Scholars602 Let f n(x) = 1=(1 n 2x) and g n(x) = nx(1 x)n, x;1Prove that ff ngand fg ngconverge pointwise but not uniformly on 0;1 Solution Show that ff ngconverges pointwise to fon 0;1, where f(x) = (1 x= 0 0 00=a (xh)2k No solutions found Rearrange Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation 0 (a* (xh)^2k)=0 Write the quadratic function in the form g (x)= a (xh)^2 k Write the quadratic function in the form g(x) = a(x−h)2 k https//mathstackexchangecom/questions//writethequadraticfunctionintheformgxaxh2k
65E 66E 67E The quadratic function f ( x) = a ( x − h)2 k is in standard form ( a) The graph of f is a parabola with vertex (____, ____) (b) If a > 0, the graph of f opens ________ In this case f ( h) = k is the _______ value of f (c) If a < 0, the graph of f opensExpress f (x) in the form a (xh)^2 k f (x)= x^24x8 Thank You!!! Write the function in the form f(x)=a(xh)^{2}k by completing the square Then identify the vertex q(x)=2 x^{2}12 x11
Let's start with an easy transformation y equals a times f of x plus k Here's an example y equals negative one half times the absolute value of x plus 3 Now first, you and I ide identify what parent graph is being transformed and here it's the function f of x equals the absolute value of x And so it helps to remember what the shape of thatAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators Well, we have coeff of x^2 a = 3 coeff of x 2 a h = 6 → 2*3*h = 6 → 6h = 6 → h = 1 constant;




Rewrite The Following Quadratic Functions In Chegg Com
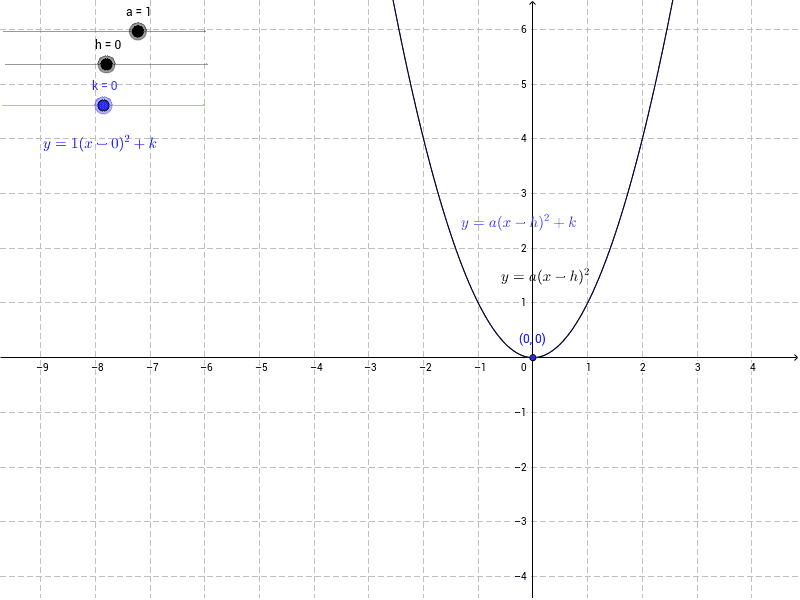



Investigating The Graph Of Y X H 2 K Geogebra
By (312), his a monomorphism, so we mayidentifyFwithasubfieldofE To prove (3), note that ifm(X)=h(X)k(X) withdeghanddegklessthandegm, tex\bf \qquad \textit{parabola vertex form}\\\\ \begin{array}{llll} y=a(x{{ h}})^2{{ k}}\\\\ x=a(y{{ k}})^2{{ h}} \end{array} \qquad\qquad vertex\ ({{ hSolution for Write the function in f(x) = a(x − h)2 k form Determine the vertex and the axis of symmetry of the graph of the function f(x) = 9x2 54x




Vertex Form Introduction Video Khan Academy




The Graph Of F X Ax 2 All Quadratic Functions Have Graphs Similar To Y X 2 Such Curves Are Called Parabolas They Are U Shaped And Symmetric With Ppt Download
If a horizontal line intersects the graph of f(x)inmorethanonepoint, then f(x)isnotonetoone The reason f(x)wouldnotbeonetooneisthatthegraphwouldcontain two points that have the same second coordinate – for example, (2,3) and (4,3) That would mean that f(2) and f To find f (xh) substitute x = x h into the function f (x h) = (x h)2 − 2(x h) 5 now distribute the brackets f (x h) = x2 2hx h2 − 2x − 2h 5 which may be expressed as f (x h) = x2 2x(h −1) h2 − 2h 5 Answer linkThe discriminant in the Quadratic Formula is b 2 – 4ac Take the negative of this to get the reverse of the subtraction –(b 2 – 4ac) = 4ac – b 2 The formula for h has a denominator of 2a;




Ch 7 Tutoring Notes Quadratics




Unit 5 Quadratic Functions Flashcards Quizlet
K In this lesson you will learn about graphs of equations of the form y = a ( x − h) 2 k For example, you will look at equations such as y = 3 x 2, y = − 2 x 2, and y = 2 ( x 1) 2 3, and compare them to y = x 2 You will also learn about roots of quadratic equations and how the values of a, h, and k affect the number of rootsThe standard form of a quadratic function presents the function in the form f (x)= a(x−h)2 k f ( x) = a ( x − h) 2 k where (h, k) ( h, k) is the vertex Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function The standard form is useful forSOLUTION solving quadratic functions of the form f(x)=a(xh)2k(that 2 is a squared) i know how to get the value of a,h,k, but i dont know what they mean when they say choose some valu




Finding Features Of Quadratic Functions Video Khan Academy



1
Where we let f(x) = p1 xThen by part(a), lim n!1 1 p n k=1 1 p k = Z 1 0 dx p x = 2 6(a)Let fbe a continuous real valued function on a;b Show that there exists a c2a;b such that f(c) = 1 b a Z b a f(t)dt Solution By the fundamental theorem of calculus F(x) = Z x a f(t)dt is di erentiable on a;b and F0(x) = f(x) ByThusE=FX/Iisafieldby(243) Wehaveaproblematthis point because F need not be a subset of E, but we can place an isomorphic copy of F inside Evia the homomorphism ha→ aI; f(x) = x^2 The vertex of the function g(x) is at (9, 8) The values of h and k is the value of x and y in the vertex's coordinates which are 9 and 8, respectively




Calgebra A1 8 4 Graphing F X A X H 2 K Youtube




Standard Form To Vertex Form Without Completing The Square Method Algebra 2 Youtube
Shifting functions introduction The graph of y=f (x)k (where k is a real number) is the same as the graph of y=f (x) only it's shifted up (when k>0) or down (when k1 P a g e Algebra 1 Unit 7 Exponential Functions Notes 1 Day 1 Transformations of Exponential Functions f(x) = a(b)xh k Describe the transformations of each variable in the table> 1 Taylor polynomials > 11 The Taylor polynomial Example Find a quadratic polynomial p 2(x) to approximate f(x) near x= a Since p 2(x) = b 0 b 1xb 2x2 we impose three conditions on p 2(x) to determine the coefficientsTo better mimic f(x) at x= awe require



Graphing Quadratic Functions




3 Ways To Find The Inverse Of A Quadratic Function Wikihow
K=1 f k n ;F (x) = a x (b/2a) 2 (4ac b 2 )/ (4a) With a couple of substitutions, this can be written in the new standard form f (x) = a ( x h ) 2 k where h = b/ (2a) and k = (4ac b 2) / (4a) Do not worry about what k is, but you might want to memorize the value for h The xcoordinate of the vertex is b/ (2a)A quadratic function is a polynomial function of degree two The graph of a quadratic function is a parabola The general form of a quadratic function is f(x) = ax2 bx c where a, b, and c are real numbers and a ≠ 0 The standard form of a quadratic function is f(x) = a(x − h)2 k where a ≠ 0



Graphing Quadratic Functions




Quadratic Function Formulas Definition Graphs Examples
The quadratic function f(x) = a(x − h)2 k is in standard form (a) The graph of f is a parabola with vertex (x, y) = (b) If a > 0, the graph of f opens In this case f(h) = k is the value of f (c) If a < 0, the graph of f opens In this case f(h) = k is the value of f please show step by stepIf the equation is y = 2(x 1) 2 5, the value of h is 1, and k is 5 If the equation is y = 3(x 4) 2 6, the value of h is 4, and k is 6 To Convert from f (x) = ax 2 bx c Form to Vertex Form Method 1 Completing the Square To convert a quadratic from y = ax 2 bx c form to vertex form, y = a(x h) 2 k, you use the process ofFor instance, when D is applied to the square function, x ↦ x 2, D outputs the doubling function x ↦ 2x, which we named f(x) This output function can then be evaluated to get f(1) = 2, f(2) = 4, and so on Higher derivatives Let f be a differentiable function, and let f ′ be its derivative



Quadratic Function




U4 2 5 Funcion De La Forma F X A X H 2 K Parte 2 Youtube
Plugging these values into the general form f(x) = a f b(x − h) k where f(x) = , we get f(x) = 4 3 This can be simplified to f(x) = 3 _____ The mapping rule is useful when graphing functions with transformations Any point (x, y) of a parent function becomes (Solution for f (x)=a (xh)2k equation Simplifying f (x) = a (x 1h) * 2 k Multiply f * x fx = a (x 1h) * 2 k Reorder the terms fx = a (1h x) * 2 k Reorder the terms for easier multiplication fx = 2a (1h x) k fx = (1h * 2a x * 2a) k fx = (2ah 2ax) k Solving fx = 2ah 2ax k Solving for variable 'f'Theorem 24 Let {f n} be a sequence of measurable functions defined on EFor x ∈ E, set g(x) = sup n f n(x) and h(x) = limsup n f n(x) Then g and h are measurable Proof We need only to show that g is measurable since the measurability of h comes



In Vertex Form Y A X H 2 K Which Letter Indicates A Stretch Change In Width Quora




8 4 Graphing F X A X H 2 K Youtube
Ah ^2 k = 2 → 3* (1^2) k = 2 → 3 k = 2 → k = 5 Hence a h k = 3 1 5 or a h k = 1 Alan Post New AnswerVertex (1,2) yintercept (0,1) xintercept , 015 Explanation y = a ⋅ (x − h) 2 k is the equation of parabola, with vertex (h,k) y = 3 x 2 6 x 1 = 3 ⋅ ( x 2 2 x 1 ) − 2Learn termquadratic function = f(x)=a(x h)^2k with free interactive flashcards Choose from 500 different sets of termquadratic function = f(x)=a(x h)^2k flashcards on Quizlet
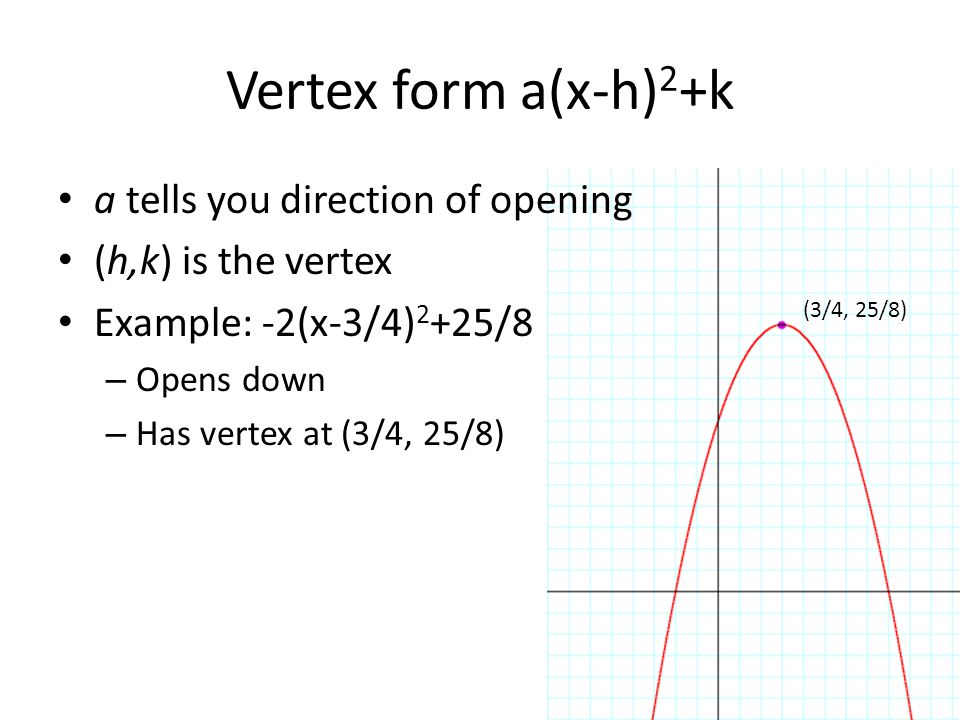



Vertex Form Ppt Download
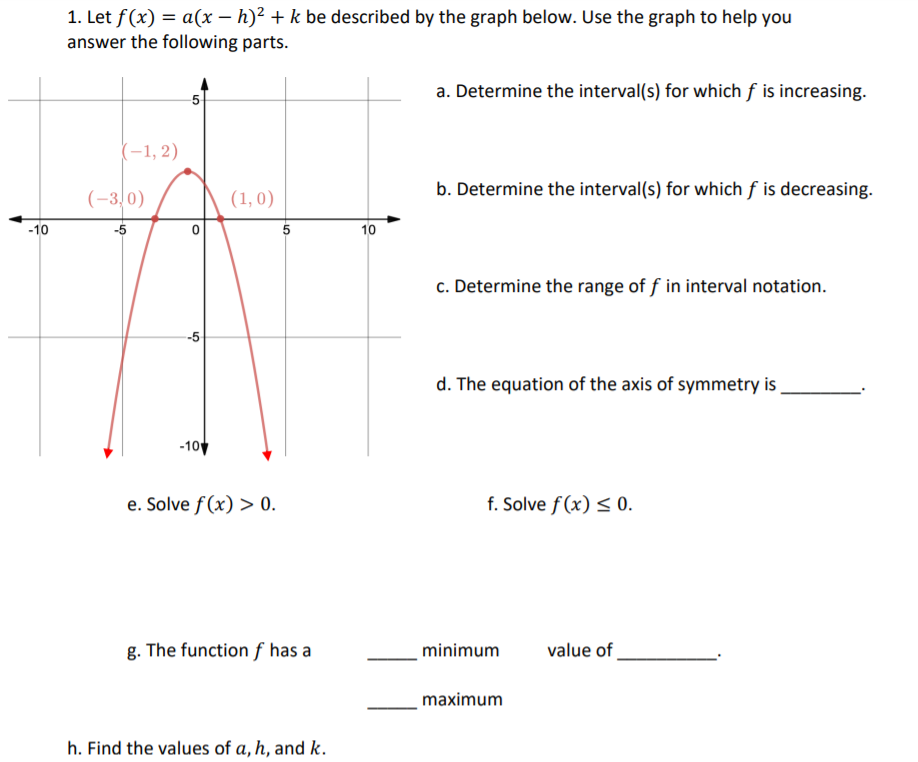



Let F X A X H 2 K Be Described By The Graph Below Chegg Com
Tema Funciones Cuadráticas f(x) = a(x – h)2 k Descripción Las funciones cuadráticas f(x) no siempre están en el formato a(x – h)2 k Para escribirlas así debemos completar el cuadrado Este formato es conveniente para el trazado de la gráfica, ya que podemos trasladarlasSolution for Write the function in f(x) = a(x − h)2 k form Determine the vertex and the axis of symmetry of the graph of the function f(x) = 5x2 30xGraphing f (x) = a(x − h)2 k The vertex form of a quadratic function is f (x) = a(x − h)2 k, where a ≠ 0 The graph of f (x) = a(x − h)2 k is a translation h units horizontally and k units vertically of the graph of f (x) = ax2 The vertex of the graph of f (x) = a(x − h)2 k is (h, k), and the axis of symmetry is x = h h f(x) = ax2 y x f(x) = a(x − 2h) k k (h, k)
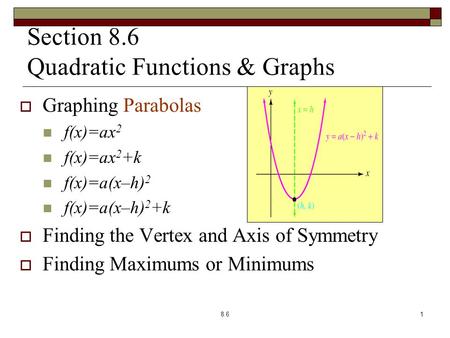



Transformations Review Vertex Form Y A X H 2 K The Vertex Form Of A Quadratic Equation Allows You To Immediately Identify The Vertex Of A Parabola Ppt Download
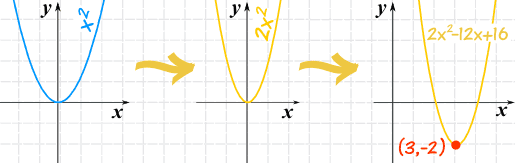



Graphing Quadratic Equations
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorAnalysing the given quadratic function f(x) = a(x−h)2k f ( x) = a ( x − h) 2 k is in standard form,we have (a) The graph of f is a parabola with vertex See full answer belowLESSON 2 Graphing Quadratic Functions in Standard Form f(x)=ax^2bxcLESSON 3 Graphing Quadratic Functions in Vertex Form f(x)=a(xh)^2 kLESSON 4 Graphing Quadratic Functions in Intercept Form f(x)= a(xp)(xq)LESSON 5 Comparing and Graphing Quadratic Functions in Different Forms LESSON 6 Completing the Square of a Quadratic Function




Graphing Parabolas




What Is Vertex Form Example Get Education
Solution For x 6˘0, jxj is a differentiable function with derivative sgn(x) ˘1 if x ¨0 ¡1 if x ˙0 Thus by the chain rule in the first line and by the product rule in the second line, f 0(x) ˘3jxj2 sgn(x) ˘3xjxj f 00(x) ˘3jxj¯3x sgn(x) ˘3jxj¯3jxj˘6jxj Checking the cases for x ˘0 by hand, we have f 0(0) ˘ lim h!0 f (x¯h)¡ f (x) h ˘ lim Substitute ah and a for x in the formula for f(x) and simplify to find (f(ah)f(a))/h = 2a 2 h >f(x) = x^22x3 Then (f(ah) f(a))/h =(((ah)^22(ah)3I assume mathg(x)=3\text{ }x/math is poorly formatted as it is meant to be written as mathg(x)=3^x/math The graph of mathg(x)/math looks like The




Funcion Cuadratica De La Forma X H 2 K Geogebra
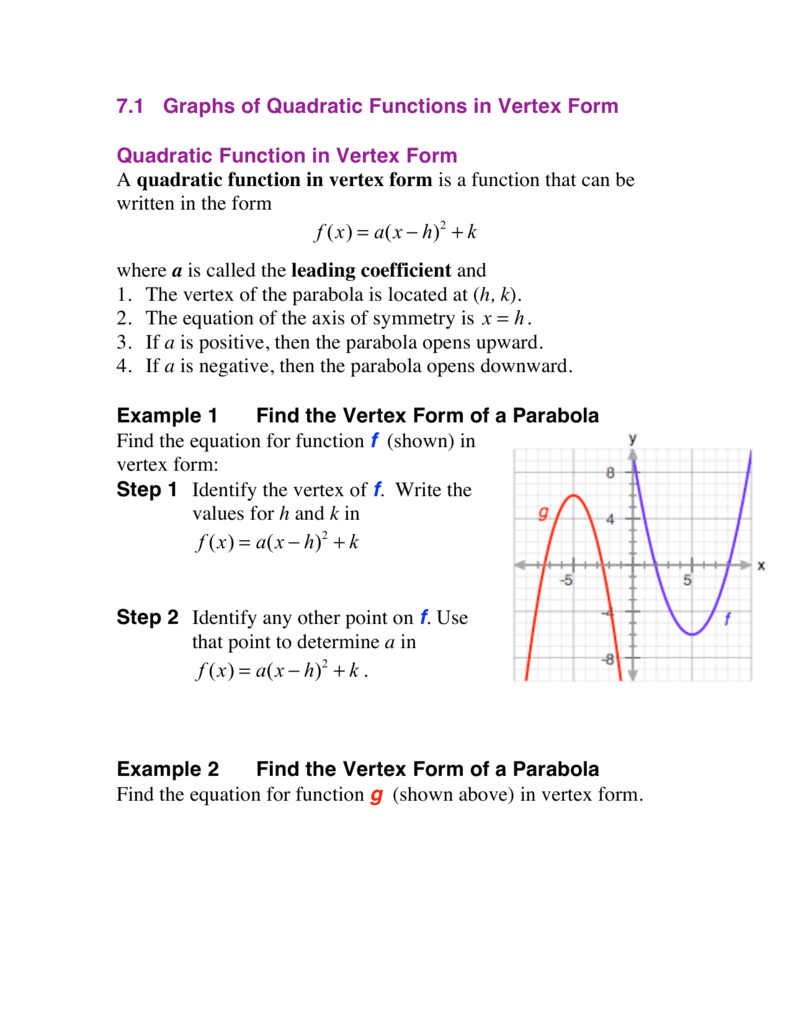



F X A X H 2 K F X A X H 2 K F X A X H 2 K
Eigenvalue k Prove it A f(x) = k f(x) A cf(x) = c Af(x) = c kf(x) = k cf(x) To specify the type of eigenfunction of d/dx more definitively, one can apply a physical constraint on the eigenfunction, as we did with the Particle in a Box c ekx must be finite as x → ∞ The most general k is a complex number k = a ib
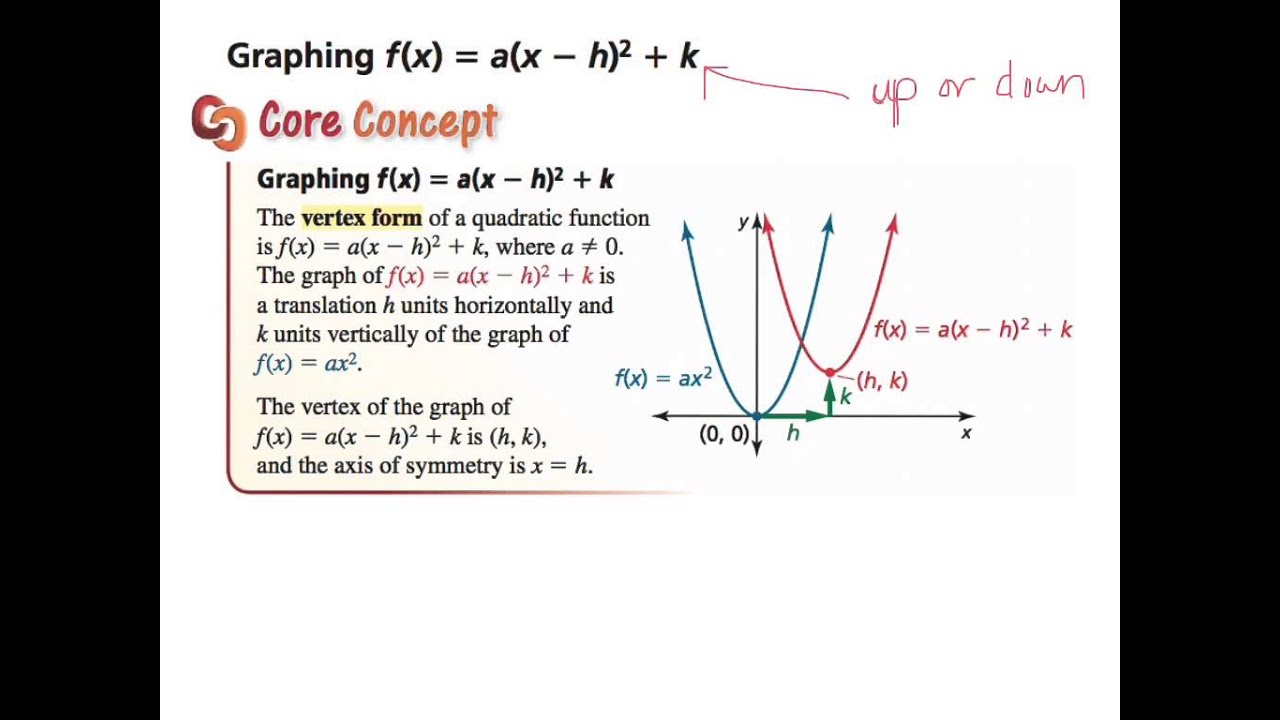



7th Section 8 4 Graphing F X A X H 2 K Youtube



Solution Write The Quadratic Function In The Form F X A X H 2 K Find The Vertex And Graph The Function A F X X 2 6x B F X X 2 4x 1 C F X 3x 2 10x 2
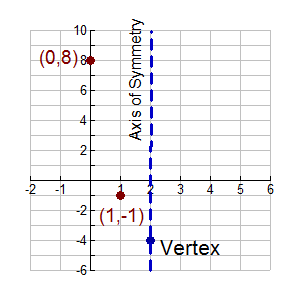



Vertex Form Of Quadratic Equation Mathbitsnotebook A1 Ccss Math




Ex Write Ax 2 Bx C In The Form A X H 2 K Negative A Youtube
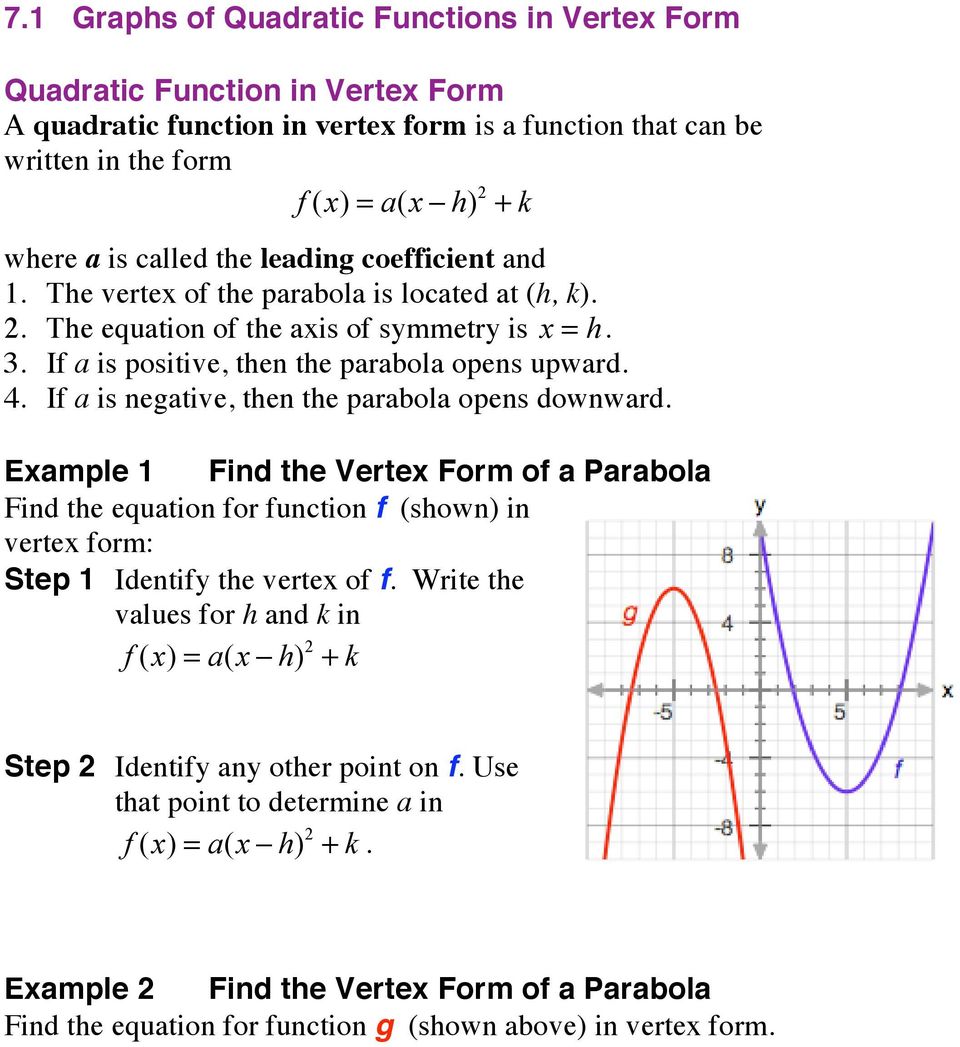



7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download




Quadratic Function Wikipedia
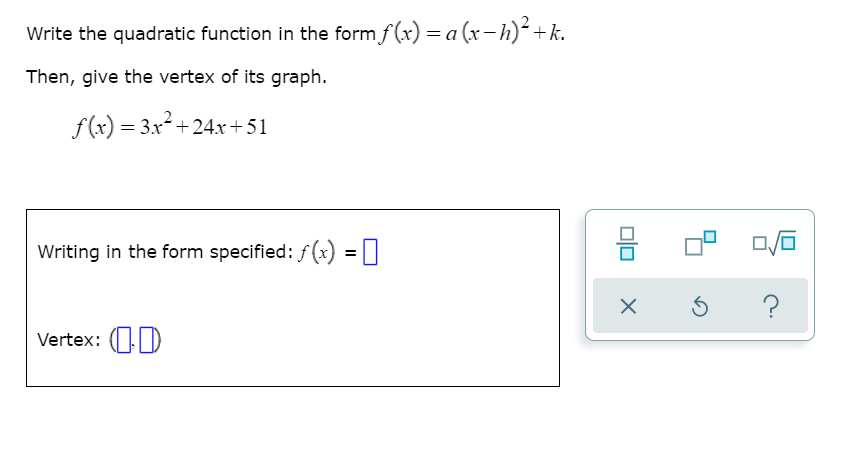



Answered Write The Quadratic Function In The Bartleby




Answered Create A New Function In The Form Y Bartleby
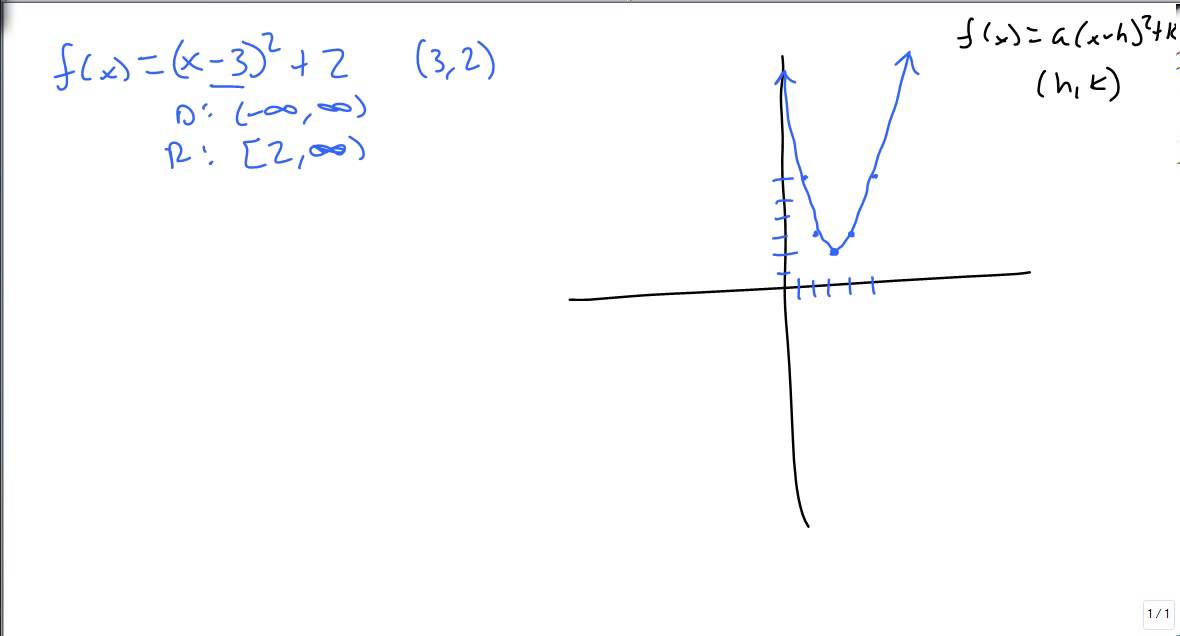



Graph By Transformations F X A X H 2 K Youtube




Quadratic Functions Ppt Download




Quadratic Functions
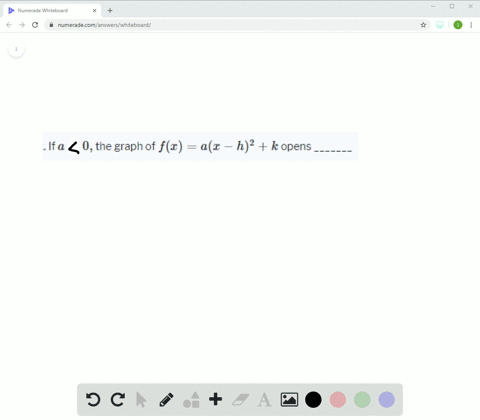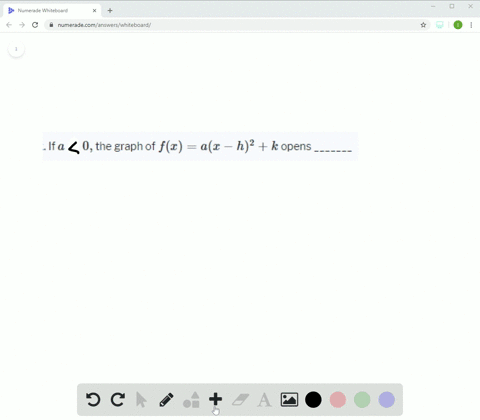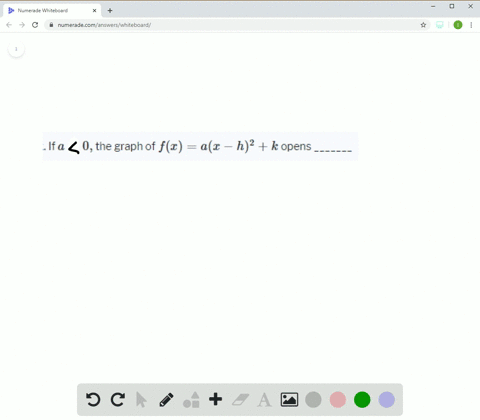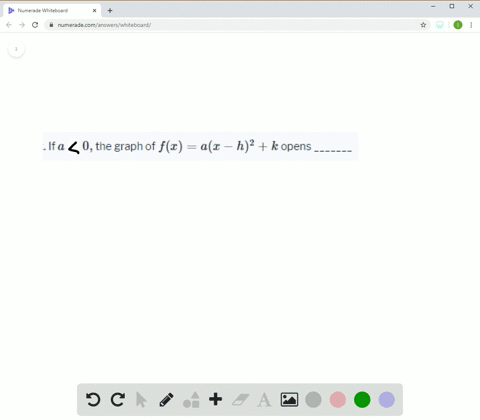



Solved Fill In The Blank If A 0 And F X A X H 2 K Then K Is The Value Of The Function



Solved Use The Graph Of A Quadratic Function F To Write Its Formula As F X A X H 2 K F X Course Hero




Quadratic Functions
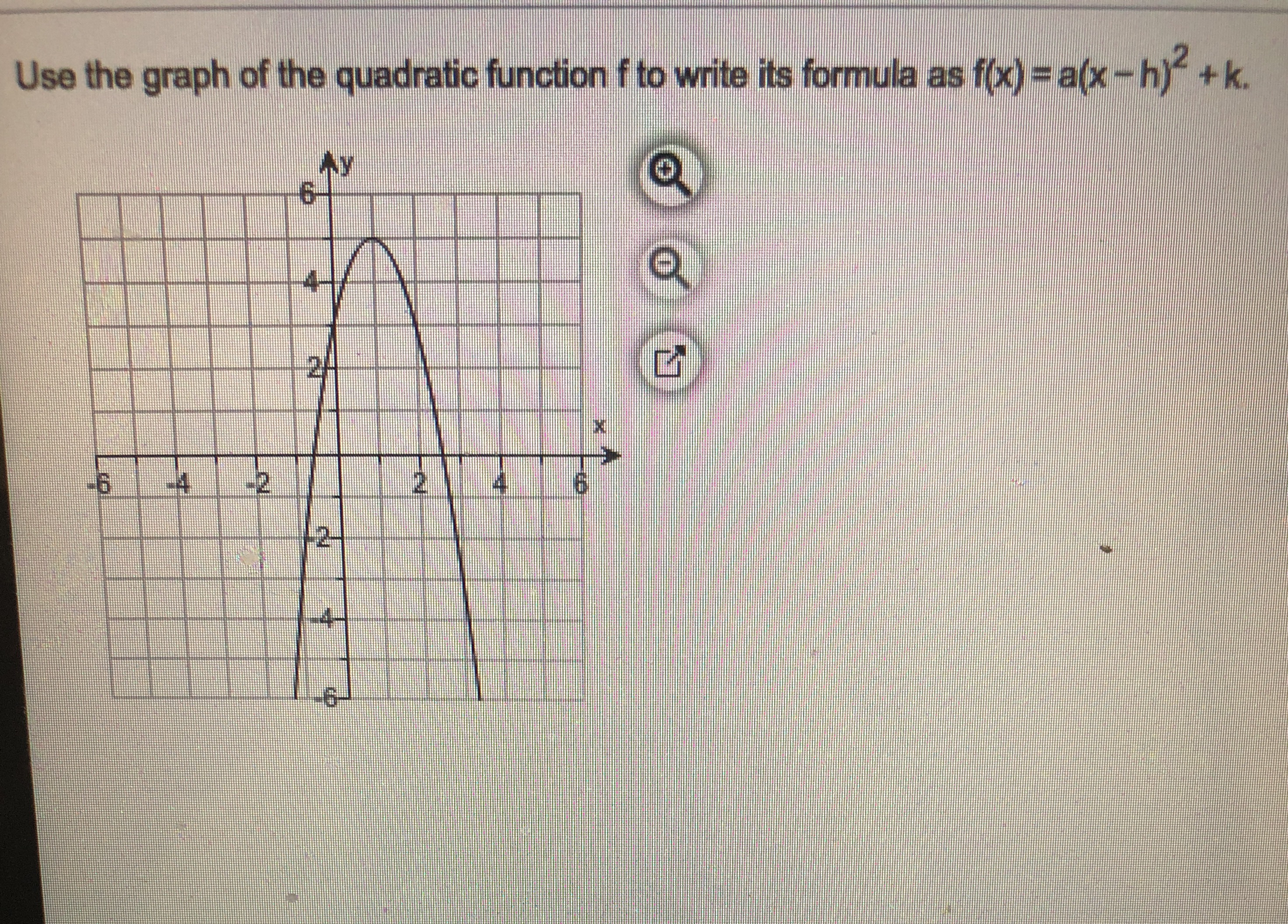



Answered Use The Graph Of The Quadratic Function Bartleby




Quadratic Function




Transform The Following Quadratic Functions In The Form F X A X H 2 K Determine The Values Of A H Brainly Ph




Graphing Parabolas



Solved The Graph Shows G X Which Is A Translation Of F X X 2 Write The Function Rule For G X Write The Answer In The Form A X H 2 K Course Hero



In The Following Exercises Write The Quadratic Function In F X A X H 2 K Form Whose Graph Is Shown Bartleby




Ex Write Ax 2 Bx C In The Form A X H 2 K Negative A Youtube



Www Hackensackschools Org Site Handlers Filedownload Ashx Moduleinstanceid 1615 Dataid Filename Vertex form transformations notes day 1 Pdf




How To Write Quadratic Functions Video Lesson Transcript Study Com




Changing A Quadratic Function Into Vertex Form Youtube



Solution The Graph Of F X X H K Contains The Points 6 2 And 0 2 The Graph Has A Vertex At H 5 Describe How To Find The Value Of H Then Explain How This Value Translates




3 Ways To Find The Maximum Or Minimum Value Of A Quadratic Function Easily




Ppt Quadratics Of The Form Y A X H 2 K Powerpoint Presentation Id



Please Help Write The Quadratic Function In The Form F X A




Answered Use The Graph Of The Quadratic Function Bartleby



Solved Use The Vertex H K And The Point On The Graph Xy To Find The Standard Form F X A X H 2 K Of This Equation Quadratic Function Course Hero




Mathematics Learners Material Module 2 Q



Completing The Square Step By Step Chilimath




Quick Review Before Hw Quiz Y A X H 2 K Form Vertex H K Axis X H Up If A 0 Down If A 0 Ex Y X 1 2 4 Y 1 X 1 2 4 A 1




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21



Graphing Y A X H K Youtube



Staffweb Psdschools Org Eharding Alg1v Bigideasch 8 A1v8 4notesgraphingf A Xh K Pdf



5 2 Quadratic Functions Mathematics Libretexts




Quadratic Formula Calculator




Write The Quadratic Function In F X A X H 2 K Form Whose Graph Is Shown F X Brainly Com




Quadratic Functions Ppt Download



Sections 6 And 8 Quadratics Part 2 And Polynomial Functions




Solved For F X A X H 2 K In What Quadrant Is




The Vertex Form Of A Quadratic Function Is F X A X H 2 K What Is The Vertex Of Each Function Brainly Com



Solution Write The Given Expression In The Form F X A X H 2 K Identify The Vertex F X 6 5x 10x 2



1




I Need To Write The Given Function In The Form Of Chegg Com




Quadratic Functions And Models Ppt Video Online Download




Quadratic Functions




The Vertex Form Of A Quadratic Function Is F X A X H 2 K What Is The Vertex Of Each Function Brainly Com
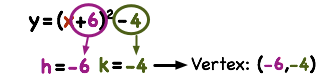



How Do You Convert A Quadratic From Standard Form To Vertex Form By Completing The Square Printable Summary Virtual Nerd




Quadratic Functions
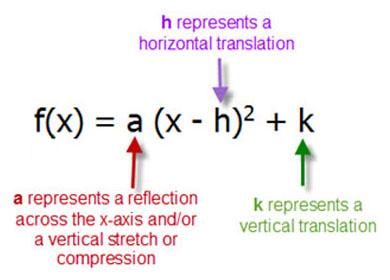



Untitled Document




Graphing Parabolas




Quadratic Functions




3 Ways To Find The Maximum Or Minimum Value Of A Quadratic Function Easily
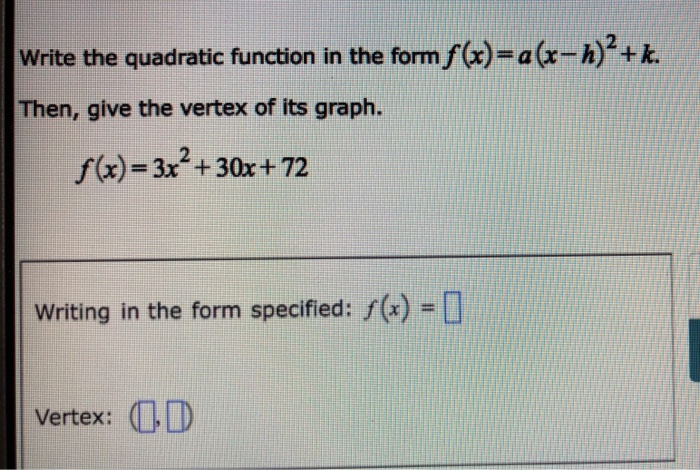



Write The Quadratic Function In The Form X A Chegg Com




2 4 Quadratic Functions Ppt Download




Absolute Value Graph And Function Review Article Khan Academy




Quadratic Functions



The Parent Function Of The Function G X X H 2 K Is F X X 2 The Vertex Of The Function G X Is Brainly Com




The Following Graph Of F X X2 Has Been Shifted Into The Form F X X H 2 K Brainly Com




Modeling Quadratic Change Flashcards Quizlet




How To Graph A Quadratic Equation 10 Steps With Pictures




Write The Quadratic Function In The Form F X Chegg Com



Www Math Tamu Edu Brlynch 150fall17 Notes 150 5 4 Pdf




Vce Mathematical Methods Units 1 And 2 4g Graphing Quadratic Functions
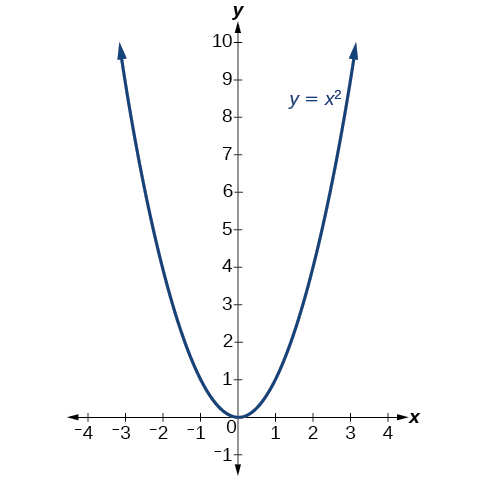



5 1 Quadratic Functions Mathematics Libretexts
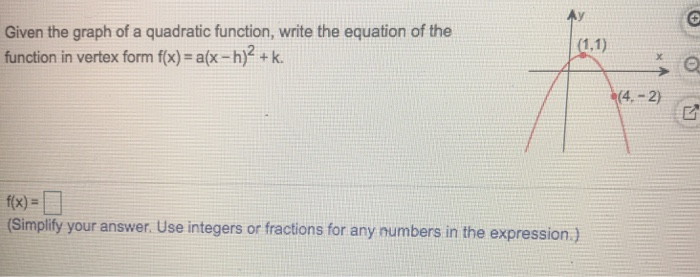



Given The Graph Of A Quadratic Function Write The Chegg Com
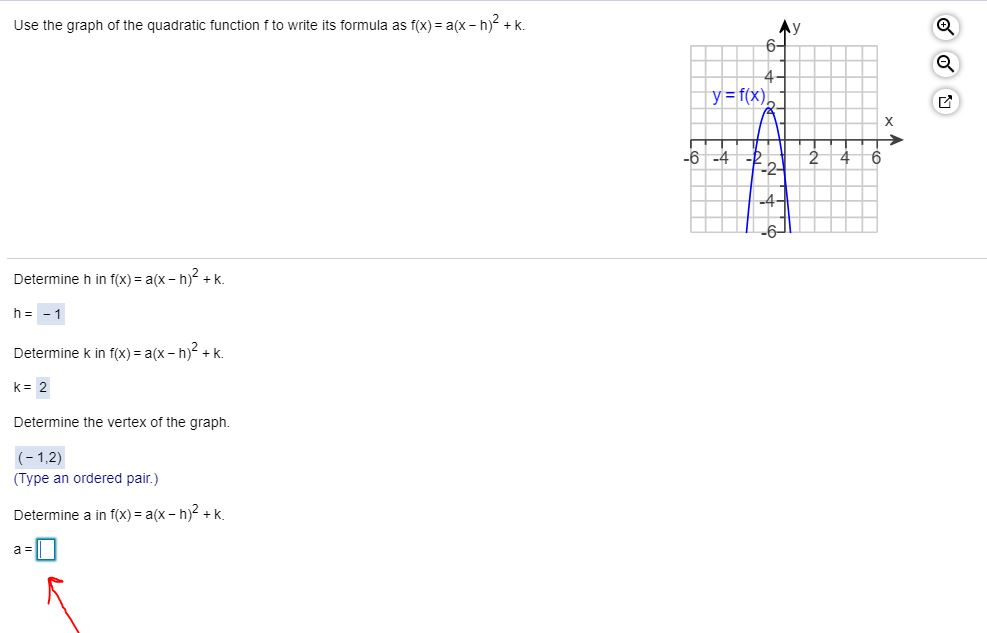



Use The Graph Of The Quadratic Function F To Write Chegg Com




Quadratic Function Formulas Definition Graphs Examples



Write The Quadratic Function F X X2 2x 6 In The Form F X A X H 2 K By Completing The Square And Ii Graph The Function Submit Graph Need Enotes Com



1




Quadratic Functions




How To Graph A Quadratic Equation 10 Steps With Pictures




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21




6 6 Analyzing Graphs Of Quadratic Functions




Graphing Quadratic Equations
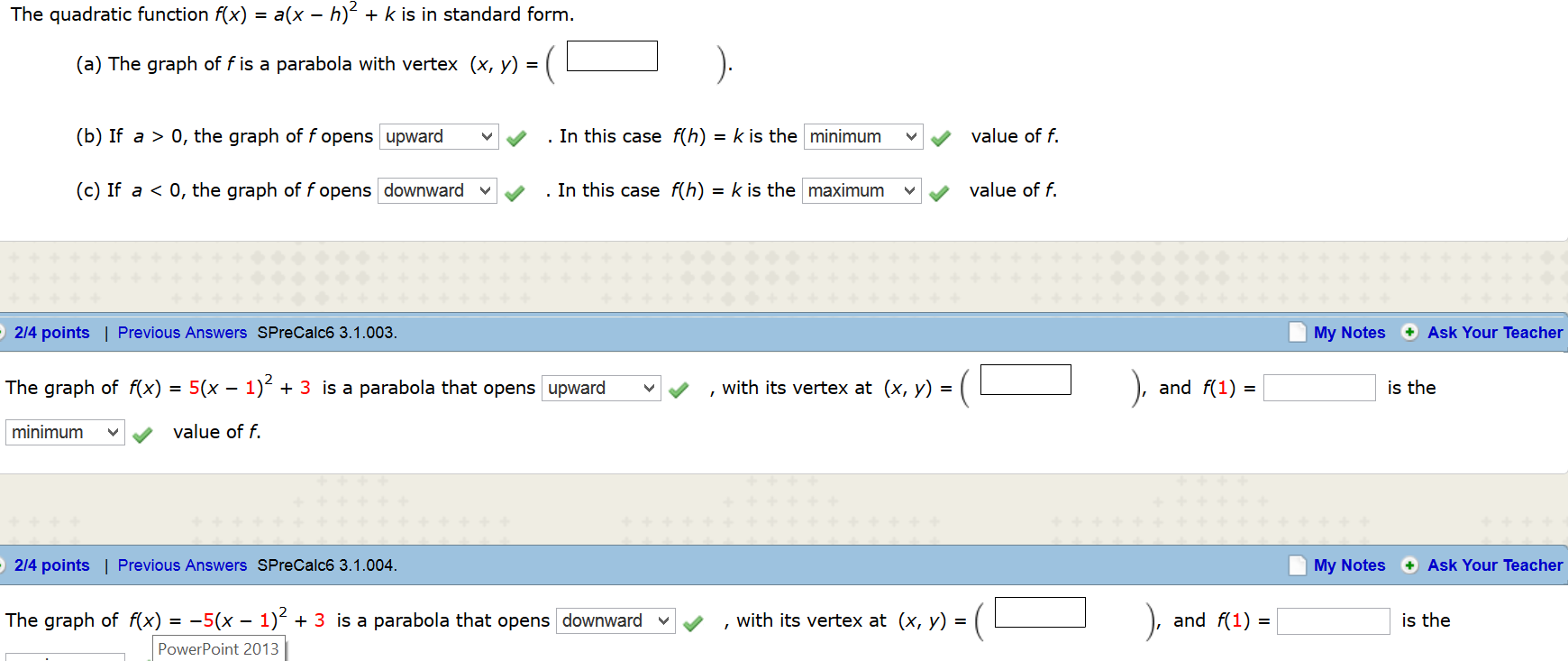



The Quadratic Function F X A X H 2 K Is In Chegg Com



0 件のコメント:
コメントを投稿